AB Testing Optimisation with a Toy Dataset
Welcome back to my second blog post on the Explore versus Exploit dilemma. To further highlight that concept, we will be using a case study of A/B testing optimisation.
As a recap, “explore versus exploit” is part of a decision-making framework under limited resources. Each unit of resource can be spent either on exploring to obtain more information on the performance of a version (in A/B testing context), or on exploiting the version that has the best performance. With optimisation, one can minimise the wasted resources spent on a lower yielding version, and investing more in the higher performance version.
Today’s topic will cover a possible research scenario for a mobile company looking at optimising their AB testing methodology.
Data:
The dataset “cookie-cats.csv” was obtained from a Kaggle Public Dataset upload. It originated from a project task under Datacamp as part of a typical AB testing project. However, my goal is different as I wish to optimise the AB testing methodology using algorithms.
Background/Description of dataset:
- User data was captured from a game called Cookie Cats, which has a typical progression in which users solves the puzzle on each stage to progress.
- The dataset was originally for an A/B testing of a control versus variant version. The difference between both versions involves the placement of a “gate” at either Stage 30 or Stage 40 of a user’s progression.
- Placing a gate at a certain stage will force the user to choose between the following actions:
- Wait for some time before they can progress
- To make an in-app purchase and immediately resume their game progression.
- Descriptions of the columns data are as shown:
- “userid”: Unique user IDs for tracking their behaviour. Each user is treated as an observation.
- “version”: The label for the control group (“gate_30”) versus variant group (“gate_40”).
- “sum_gamerounds”: Number of games the user played within the first 14 days.
- “retention_1”: Boolean data input that represents if a user came back to play 1 day after game installation.
- “retention_2”: Boolean data input that represents if a user came back to play 7 days after game installation.
- For this project, I will use “retention_7” as it is a good measure of players returning after an extended period.
Algorithms
There are 4 algorithms that will be evaluated:
- Random Search: Randomised exploration of both versions
- Epsilon Greedy: Randomised exploration will be done at a standard 5 % (or epsilon) of the time. The remaining 95% will be used to exploit the version with the current highest performance.
- Upper Confidence Bound (UCB): UCB will favour the version with the highest potential yield. This is defined by the sum of the current average performance with a parameter that accounts for unexplored uncertainty. The value of the parameter decreases with testing progression, which reduces the tendency for exploration.
- Thompson Sampling: Using the beta distribution, both versions will draw a random sample based on their current beta parameters. This allows for the possibility of exploring low yield versions with high uncertainty, and exploiting high yield versions with low uncertainty. The version with the highest sample results will be favoured.
Regret
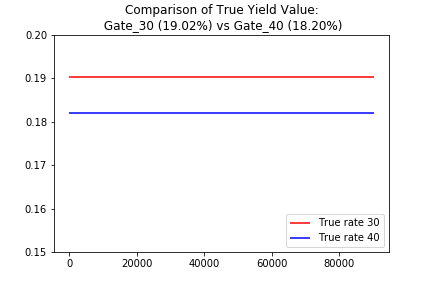
Evaluating the algorithms will be based on a concept called regret. Since “gate_30” has a higher retention rate compared to “gate_40”, the “regret” metric can be defined as the excess number of trials beyond the pure exploitation of the “gate_30” portion of the dataset. The lower the value is, the better the performance of the algorithm.
|
True yield comparison between both versions
|
Simulation Methodology
Each algorithm was simulated with 3 sets of 10 simulations:
- Each set represented simulations with varying ratios of the overall data (namely, 25%, 50%, and 100%).
- Across each set of 10 simulations, seeds were varied to provide 10 randomised datasets. Every algorithm faced the same randomised dataset in each iteration to ensure fairness of the experiment.
Analysis
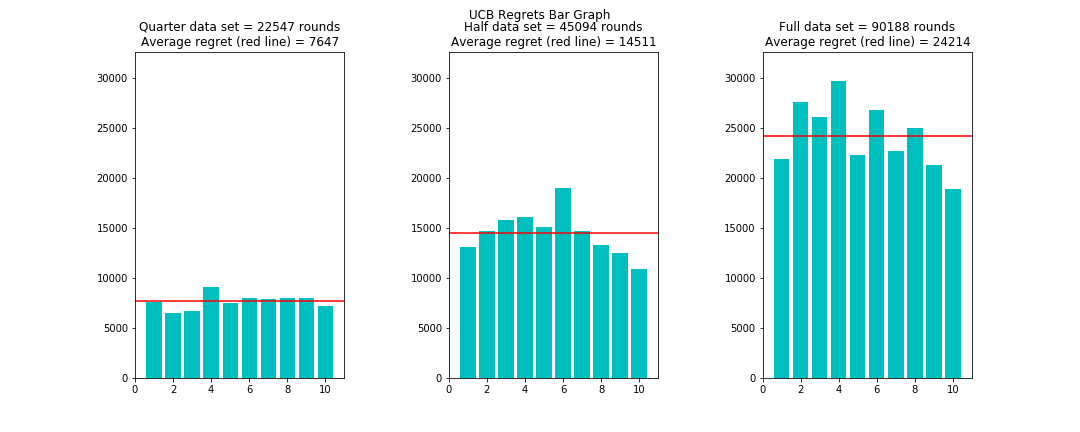
Both Random Search and UCB performed on a poorer scale compared to Epsilon-Greedy and Thompson Sampling across varying dataset sizes.
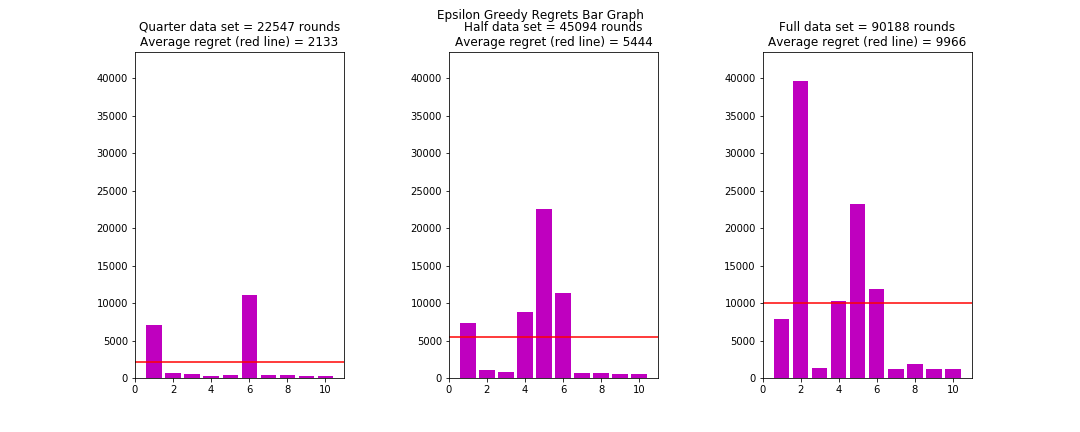
The algorithm with the least amount of regret based on the full data set is the Thompson Sampling algorithm with an average of 8983. However, the Epsilon- Greedy algorithm is not far behind with an average of 9966. In fact, with smaller datasets (25% and 50%), Epsilon-Greedy outperforms Thompson Sampling. An explanation could be that with a smaller dataset, there is still high uncertainty on both versions’ performance in the context of Thompson Sampling, and thus it tends to be in the “exploration” mode. With a bigger dataset, the Thompson Sampling algorithm will eventually switch to an “exploitation” mode which helps it overtake the Epsilon-Greedy algorithm eventually.
Both algorithms also had relatively more variation in their performance compared to the other two. Epsilon-Greedy tends to suffer from extreme regret if the datasets were randomised to be unfavourable. In a particular case (Simulation 2 of Full dataset), the Epsilon-Greedy algorithm ended with a high regret of around 40,000 rounds. The highest regret among Thompson Sampling simulations (Simulation 4 of Full Dataset) is about 22000, which is almost half of the former.
| Random Search Regret Comparisons |

| Epsilon-Greedy Regret Comparisons |
| UCB Regret Comparisons |
| Thompson Sampling Regret Comparisons |

Conclusion
Based on the simulation methodology, it seems like Thompson Sampling is the best optimisation algorithm for a large dataset. Firstly, it tends to perform very well in terms of regret minimisation across the size of the data sets. Secondly, although it has large variations in its regret, it does not suffer badly across randomised datasets variation.
For a mobile company”, these advantages translate into critical benefits in terms of actual deployment for A/B Testing optimisation. It mitigates any risk of extreme poor performance in the event of unfavourable data variation (compared to Epsilon Greedy) and also has much faster convergence to the high performance versions (compared to Random Search and UCB).
